量化交易中为什么使用对数坐标系？

量化交易中为什么使用对数坐标系？

如何度量收益？

本源问题：衡量投资收益的最直接标准是收益百分比还是收益绝对值？

带着初始资金开仓，虽然收益或亏损的绝对值给人的感觉最为直接，但是收益或者亏损的百分比才是我们衡量一项投资水平的最重要指标；各位仔细想想是不是这个道理，百分比！

为什么选择对数？

在回答完第一个问题后，我们都明白要选择用百分比来度量投资的收益，那我们最直接的思路是直接使用百分比，还是使用其他的方法？这样会有问题吗？

我们举个例子🌰：

假设一只标的的初始价格是10；

第一天收盘价是15，相比开盘的10涨了50%；

第二天收盘价是22.5，相比开盘的15也涨了50%；

第三天收盘价是11.25，相比开盘的22.5跌了50%；

直接选择百分比可以吗？

针对这个🌰，假如我们直接使用百分比来画K线将会是如下的情况：

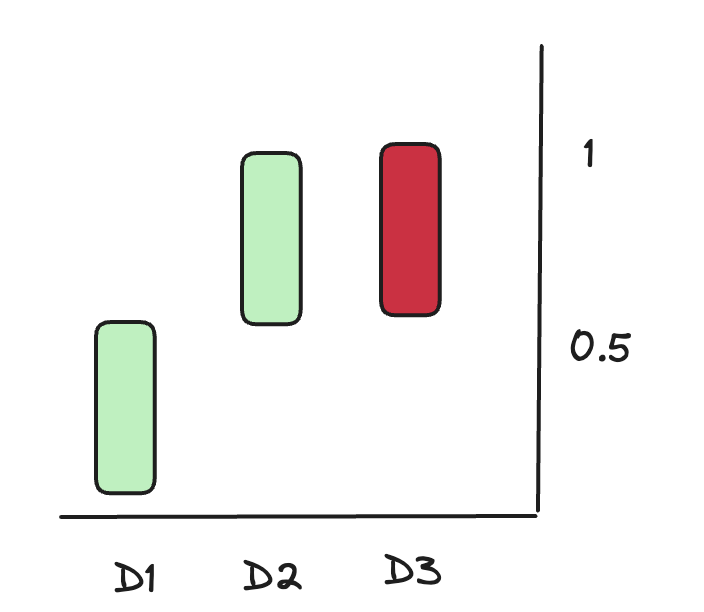图1 K线百分比坐标系

如图中所示，D1收盘涨了50%（标的价值15元），D2收盘涨了50%（标的价值22.5元），D3收盘跌了50%（标的价值11.25元）。我们发现这样的K线只能反应相对百分比，并不能体现标的的绝对价值的相对关系，也不能体现几个收盘日后我们的收益比例（如果我们在D2进场，D2离场，这张图看起来是盈亏平衡，而实际上我们是亏损了，因为D收盘价11.25低于D2的开盘价15）；

对数的几个性质

对数的几个性质：

ln P₂ - ln P₁ = ln (P₂/P₁)

ln P₂ + ln P₁ = ln (P₂*P₁)

ln 1 = 0

在x > 1的情况下，ln (1/x) < 0 但 ln x > 0

从上面的几个性质，我们发现其特性正好可以满足我们的需求（我们假设P₁是第一天的收盘价，P₂是第二天的收盘价）：

1. 行情没有涨跌的时候，标的价格变化率为1，此时 ln 1 = 0 的特性正好满足要求

2. 行情上涨时，P₂/P₁>1，此时（在x > 1时）ln x > 0特性正好满足要求，在对数坐标系上体现为上涨，且P₂/P₁ 正好就是涨幅比例，可以体现等比例上涨，直观体现投资者的收益比例；

3. 行情下跌时，P₂/P₁<1，此时（在x > 1时）ln x < 0特性正好满足要求，在对数坐标系上体现为下跌，且P₂/P₁ 正好就是跌幅比例，可以体现等比例下跌，直观体现投资者的亏损比例；

4. 我们还需要在K线中直观的看到标的绝对价值的相对关系，此时对数函数的单调性正好满足要求；

结合这些特点，我们尝试用对数坐标来画一下前面🌰中的K线：

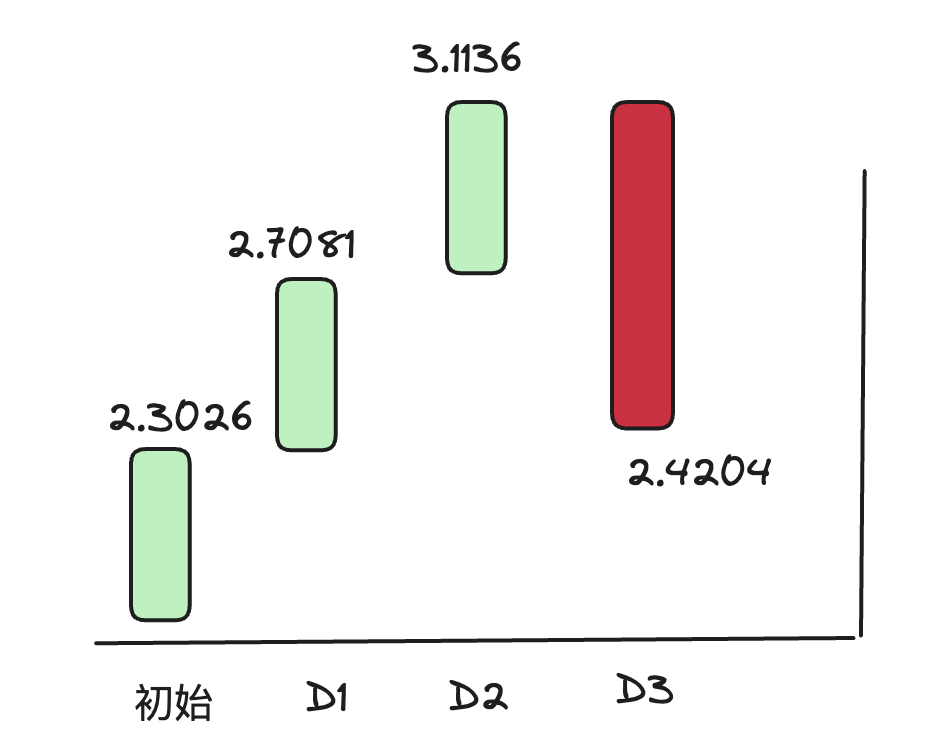图2 K线对数坐标系

我们从图2可以发现，D1、D2的涨幅50%体现在K线图中是等比例的，D3下跌后也能体现出标的绝对价值的相对关系；

综上，K线对数坐标系的优点：

1. 可以体现涨跌幅的绝对值相对关系

2. 可以体现涨跌幅百分比的比例

总结

到此为止我们理解了对数坐标系的巧妙之处。

在文章开始我们没有就绝对值坐标系做过多的解读，在这里我们可以就前面的🌰做简单调整来描述一下：

增加第四天收盘价是5.5625，相比开盘11.25跌幅50%；

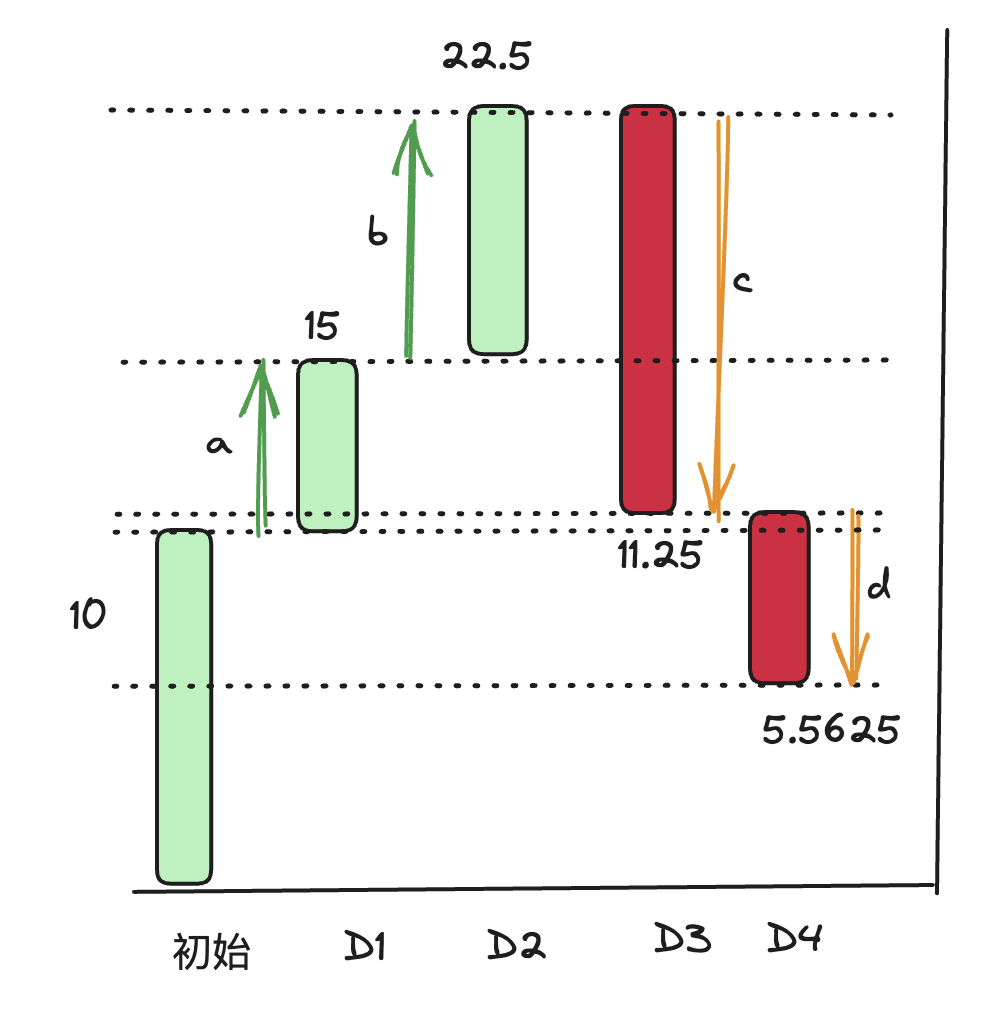图3 K线绝对值坐标系

我们回顾一下图4的过程：

1. b箭头与a箭头涨幅相同，都上涨了50%，但是由于体现出来的高度不一样，会影响投资者判断世纪涨幅

2. d箭头与c箭头都是跌幅50%，但是d箭头短会导致给投资者跌幅缩小的错觉

综上，K线绝对值坐标系会影响投资者对涨跌幅速度和降幅区间的判断。

写在最后

上述是我作为一个业余选手学习过程中根据各种资料自己推导的过程，如有不对之处，欢迎各位留言指正。